Panini FIFA Sticker Collections

My eldest son likes collecting things.  Of course all children seem to like picking up random objects and hoarding them forever, and we’ve had our fair share of leaves, stones, food wrappers and other assorted paraphernalia floating around the house until we can divert attention elsewhere and get rid of them.  But my son also really likes collecting sets of toys, books and, currently, stickers.

He first got into this during the World Cup in 2014 when I thought he was old enough to really enjoy collecting the stickers of all the players and teams that you find in the famous Panini sticker album that’s published before each competition.  I remember collecting these when I was growing up; the excitement at opening each pack to see which new players you could add to your album, along with the cut and thrust of swapping your doubles with all your mates in the school playground, sometimes getting several stickers to add to your collection in return for just one particularly valuable duplicate you had.  It never quite worked out like that with my son because none of his friends seemed to be collecting too (maybe it’ll happen in two years’ time), but we swapped stickers through a website, with the added anticipation of new stickers arriving whenever the postman appeared, and eventually completed the album.  He still looks through it regularly now.

Over the last 18 months we’ve bought a few more albums with significantly less success (the Jurassic World collection looked like a winner, after all it was a perfect marriage of stickers, dinosaurs and collecting, but our village shop stopped stocking the stickers soon after we bought it, making it difficult to buy them and removing the exciting post-school detours to get more packets each week).  I think, in general, we timed buying the albums badly so that they were near their shelf-lives by the time we jumped on board.  However, the newest album is looking in good shape and I think we’re going have a finished collection once again.

For the latest round we’ve returned to football once more with the Panini FIFA 365 2016 sticker album.  (I know there’s a lot of issues at FIFA right now; perhaps they forgot that it’s a leap year with everything else going on, or maybe they think everyone needs a day off football.  I suppose February 29th could be a football-free day, I’m really not sure…)  In some ways we’re a bit late to the party with this one too, although I’ve checked first that we can buy stickers for a while yet.  We first thought we’d do an album for the Rugby World Cup last year, but nobody produced one and, given England’s performance, the whole thing is best forgotten anyway (although we did see a great game between Japan and Samoa in Milton Keynes).  We then thought we’d do one for the European Championships this summer, but again it doesn’t look like there’s going to be one.  So we settled on this one that has some of the best club teams from across the world, as well as a few from other international tournaments.

Last time we completed an album I remember feeling like we were constantly buying stickers and doubles came fairly quickly.  When starting this, I was interested in delving more into the maths of it, to see how quickly we should expect to finish the album and what the damage to my wallet would be!  Of course I was aware of the birthday problem, which tells me roughly when doubles should appear, and the related coupon collector’s problem, which tells me how many stickers we should expect to buy to complete the whole thing, but there are three twists to this that stop it being a totally straightforward problem:

1. You get several stickers free when you buy the album;
2. You can buy up to 50 of your choice direct from Panini; and
3. You buy stickers in packs of 5 at a time, each distinct within a pack.

When I started searching for a solution to the problem, I came across a short study from the University of Geneva¹ which looks at whether certain stickers really are rarer than others (i.e. that fewer are actually printed – it seems that they are not and any perceived shortages can be put down to our intuition about the likelihood of events happening being out of sync with their actual probabilities, much like the birthday problem).  It presents a strategy for a number of friends completing albums together and swapping duplicates.  However, although their study also considers packs of 5 stickers at a time, it appears that in Switzerland you can buy boxes of 100 packs (i.e. 500 stickers) where all stickers are distinct.  In addition, this didn’t give me an equation that I could apply to my problem: namely one where the set of stickers you’re interested in is a subset of the set of all possible.

A post on StackExchange’s Cross Validated site pointed me towards another academic paper² which gives the equations I want.  Despite my best efforts at misunderstanding, I found two of them to be useful.  The first calculates the probability of fewer than n stickers being collected (from which we can obviously calculate the probability of at least n):

\[ P(X_k(A) \lt n) = \sum_{j=0}^{n-1}(-1)^{n-j+1}{l \choose j}{l - j - 1 \choose l - n}\left[{s - l + j \choose m}\bigg/{s \choose m}\right]^k\quad\quad n = 1, \cdots, l \]

where \( A \) is the set of stickers we’re interested in (\( A \subset S \), the set of all stickers available), \( l = |A| \), \( s = |S| \), we buy packs of \(m\) distinct stickers and \( X_k(A) \) is the number of distinct stickers belonging to \( A \) found in \( k \) packets.  The second equation gives the expectation:

\[ E(X_k(A)) = l \left[1 - \left(1 - \frac{m}{s}\right)^k \right] \]

In terms of my son’s album, the variables can be fixed to \( s=472 \), \( l=452 \), \( n=402 \) and \( m=5 \).  That is a total of 472 stickers (actually there’s 856 but within each pack, a single sticker corresponds to either 1, 2 or 3 numbers within the album depending on whether it is kept whole, halved or split in three (is ‘thirded’ a word?); here I’m sticking (sorry!) to calling a sticker a whole card, no matter whether it is split or not).  There’s about 20 free with the album (it’s 31, but I didn’t record whether they were singles, halves or thirds, so 20 seems to be a good enough estimate), so of the total we’re only interested in the remaining 452.  We can buy the final 50 direct, so we need to reach 402, and you get 5 stickers per pack.  We can plot the probability and expectation as we vary \( k \), the number of packets.  First the expectation.

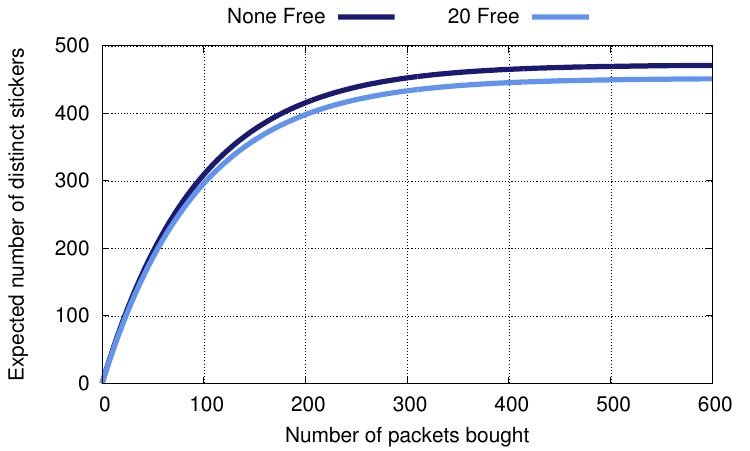To show the impact of the 20 stickers free with the album, I’ve also plotted the case where you don’t get any stickers free.  It doesn’t actually make too much difference.  You have to buy 206 packets to get an expectation of 402 stickers (for the 20-free case) or 210 packets to get an expectation of 422 stickers (when none are free).  At 50 pence per packet, that’s £103 to enable us to buy those final 50 direct and complete the album, not to mention the 628 duplicate stickers we’d be left with!

Imagine now that we couldn’t choose and buy those final 50.  You have to buy 640 packets to get an expectation of 452 stickers (for the 20-free case), or 644 to get an expectation of 472 stickers (when none are free).  That’s £320 and 2,748 redundant stickers!

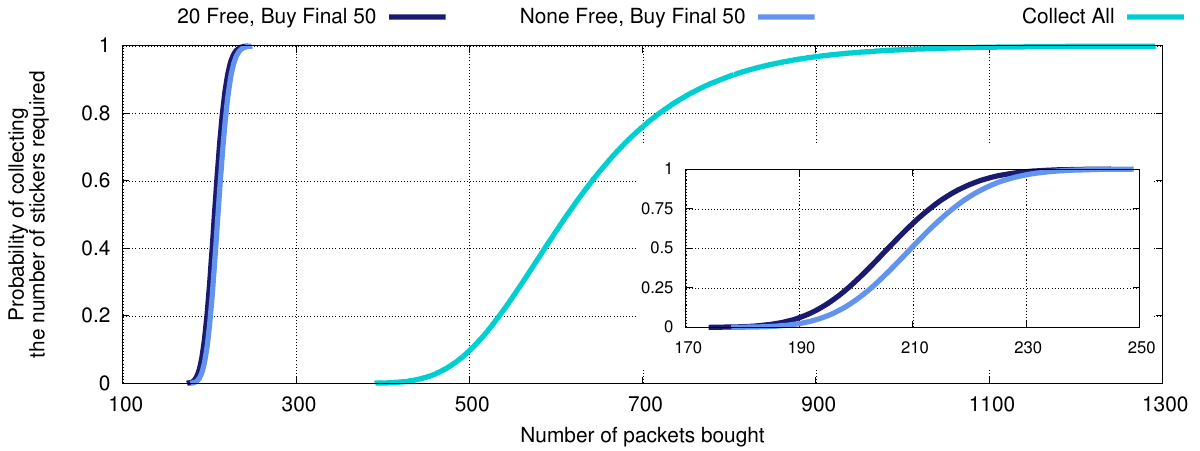
Now consider the probability of collecting those stickers.  I’ve drawn our real life case (get 20 free, buy the final 50), the situation where you don’t get any free but can buy the final 50, and a hypothetical case where you must collect all stickers by buying packets, without getting any free or having any choice in the ones you buy at the end.  Since the first two lines are close together, I’ve redrawn them in the inset graph to better show their differences.

Here it’s clear exactly what a difference being able to choose those final 50 makes.  It’s extremely hard to finish the album without them.  You need to buy 613 packets to have a 50% probability of collecting all stickers, or 790 packets to reach a 90% probability.  In contrast, my son has a 50% chance of completing his album at 206 packets (from above, recall the expectation was 402 stickers at this point) or a 90% chance at 220 packets.  He’s 99% certain to have completed it after buying 233 packets.

Of course, none of this takes into account swapping.  The website we’ve used before allows you to swap with anyone, anywhere, instead of only your mates you see day-to-day.  This adds another dimension since you generally post off stickers that you’re swapping, so you pay the price of postage rather than doing the swap for free.  I haven’t included that here.  It would be useful to know whether a swap is worthwhile, given the price of postage and the number of stickers you’ll get in return, or whether it’s better just to buy more packets, but I’ll leave working on that for another day.

Finally, you might well ask where we are with all this.  Well, as of today, my son has got 274 stickers and 97 duplicates.  I know that this doesn’t add up to a multiple of 5 – we must have lost some duplicates somewhere, or my estimate of getting 20 free was a little out.  That equates to us buying 70 packets.  We’ve got to buy at least 81 packets to have enough stickers to swap 1-for-1, so we need 11 more anyway. However, looking at the expected number of stickers for 70 packets shows that we should have only collected 248 stickers at this point (or 258 with those 20 free), so he’s a little ahead of the game.